La recta se puede definir como una línea que no sufre ningún tipo de inclinación, ni desviación, curvatura o torcedura. En Geometría la recta es una línea que une dos puntos que están ubicados en un plano, la cual está conformada por una sucesión ordenada de puntos ininterrumpidos. Junto al punto y al plano, la recta es uno de los elementos geométricos fundamentales y básicos.
Las rectas están en todas partes, se pueden observar en las rectas de un borde de la cama, de una hoja de papel, en la carretera, en un hilo/cable/cordón extendido. Una de las principales características de las líneas rectas es que estas poseen una determinada longitud y extensión.
Características de la recta
- La recta es una serie infinita de puntos que mantiene una sola dirección, o sea, no presenta curvaturas.
- Cuando se dibuja una recta, esta suele tener un comienzo y un final. Pero la verdad es que de acuerdo al concepto de esta, una reta no cuenta con un punto de origen ni con un punto de llegada.
- La recta es un elemento básico de la geometría, pues a partir de este se pueden analizar algunos conceptos más complejos, como por ejemplo los poliedros o los polígonos.
- Una recta se diferencia de una semirrecta, pues esta última es una porción recta que tienen un origen pero que se extiende hasta el infinito. Desde esta perspectiva, si se corta una resta desde uno de sus puntos, este será el comienzo u origen de una semirrecta que comenzará a extenderse de manera indefinida.
- Un segmento se diferencia de una recta, pues este es una porción de la recta que va desde un inicio hasta un final.
Tipos de rectas
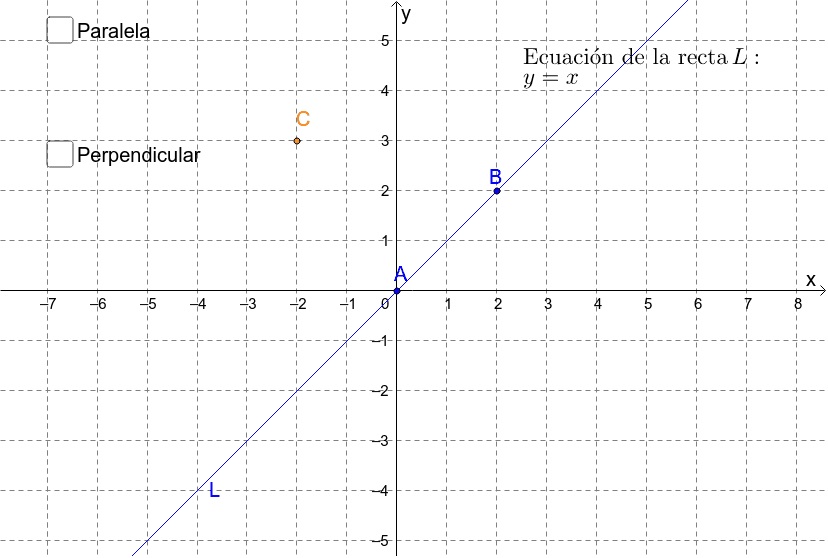
- Las rectas paralelas: Estas son aquellas líneas que no se cruzan, o sea, no existen ningún punto que forma parte y una ambas rectas, son equidistantes y tienen sus puntos a la misma distancia que la otra recta. En otras palabras, las rectas.
- Las rectas perpendiculares: Dos rectas son perpendiculares cuando se cortan y forman cuatro ángulos iguales. Por otra parte, además las rectas perpendiculares son al mismo tiempo rectas secantes.
- Las rectas secantes: Son aquellas que tienen diferentes direcciones pero que en un determinado punto se tocan.
- Las rectas secantes: Dos rectas son secantes cuando se cortan únicamente en un determinado punto, por ende, las rectas son secantes cuando solo tienen un punto en común. Por otra parte, ambas rectas deben estar necesariamente contenidas en un mismo plano.
Además de estas, las cuales son consideradas las rectas más importantes de la geometría, pero por otra parte existen otros tipos de rectas que suelen ser menos conocidas.
- Las rectas concurrentes: Son dos o más rectas, las cuales se cortan en un mismo punto, y además, están contenidas dentro de un mismo plano.
- La recta de regresión: Esta sirve para aproximar la relación numérica entre dos o variables diferentes.
- Segmento: Es el fragmento de una recta que está comprendido por dos puntos.
- Las rectas coplanares: Son dos o más rectas que permanecen dentro de un mismo plano.
- La semirrecta: Cada una de las dos partes en las cuales quedad dividida una recta al cortarla por cualquiera de sus puntos.
- La recta tangente: Esta es una recta que toca una curva en un único punto, que se le conoce como punto de tangencia.
Ecuación de las rectas
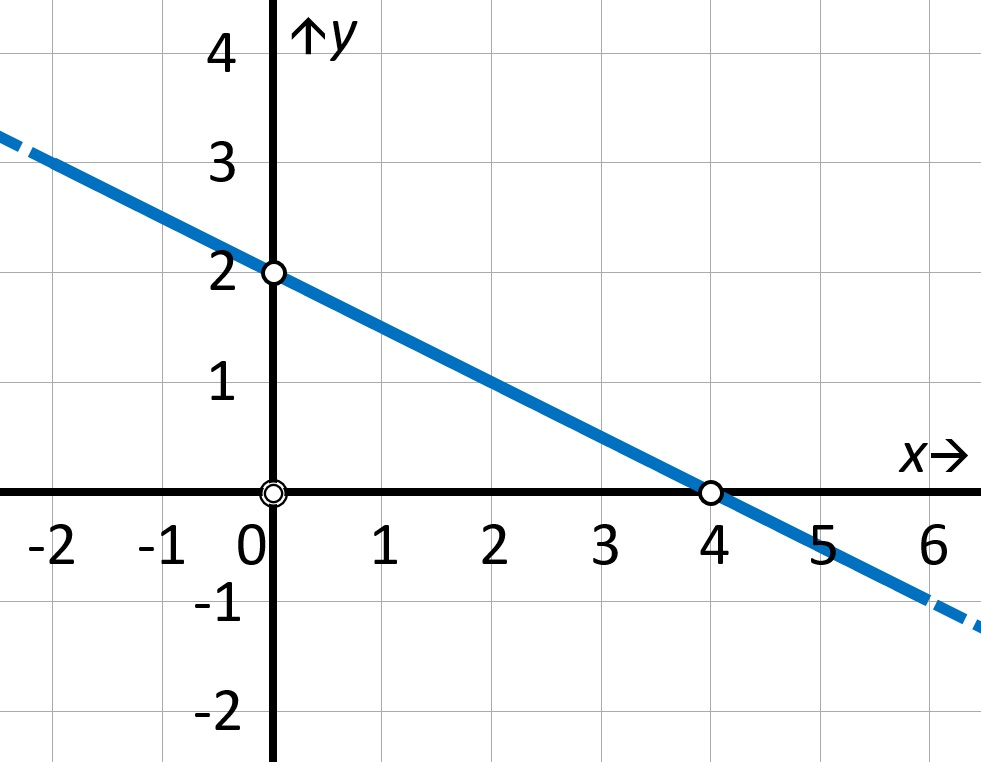
La ecuación explicita de una recta es aquella que viene dada por la siguiente expresión:
y = mx + n
- m: es la pendiente.
- n: es la ordenada de origen.
La ecuación general o implícita de una recta se puede expresar con todos los términos del lado izquierdo de la ecuación, igualados a cero (0). Esta se denomina de la siguiente forma:
Ax + By + C = 0
En caso de que una recta tenga como ecuación general Ax + By + C = 0, entonces su pendiente será igual a:
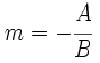
La ecuación del punto-pendiente de una recta queda perfectamente determinada debido a su inclinación, así como por un punto contenido en ella. Esto permite obtener el siguiente resultado:
Sea (x0, y0) un punto de una recta y m su pendiente, por ende la ecuación vendría siendo dada por:
Y – Y0 = (x0, y0)
Siendo esta la expresión que se denomina como la ecuación punto-pendiente de una recta.

