Una expresión algebraica se construye a partir de tres tipos de elementos básicos:
- Coeficiente (números);
- Constantes (letras al principio del alfabeto, por ejemplo: a, b, c);
- Variables (letras al final del alfabeto, por ejemplo: x, y, z).
Como ves, las constantes y variables son letras. Pero representan valores numéricos.
EXPRESIÓN ALGEBRAICA
Puede parecer un poco confuso, pero no tienes que preocuparte por esto en este momento. Durante la realización de operaciones con expresiones algebraicas, las operaciones con variables y constantes se realizan de la misma manera.
Existe una diferencia importante entre constantes y variables
- Una constante es un valor que permanece sin cambios, aunque es desconocido o indeterminado.
- Una variable es un valor que puede cambiar.
El álgebra es una rama fascinante y encantadora de las matemáticas en la que se utilizan números, formas y letras para expresar problemas. Ya sea que esté aprendiendo álgebra en la universidad o mirando un examen en particular, seguramente verá que casi todas las cuestiones matemáticas se representan en la expresión algebraica.
En consecuencia, la necesidad de convertir los problemas de palabras compuestas en expresiones algebraicas surge cuando necesitamos abordarlos.
Muchos de los problemas de expresión algebraica consisten en casos o historias cortas de la vida real. Otras son expresiones básicas como el resumen de problemas matemáticos.
De hecho, esta publicación descubrirá cómo componer expresiones algebraicas a partir de problemas de palabras sencillos, después de ese avance hacia problemas de palabras ligeramente intrincados.
MÁS INFORMACIÓN SOBRE LA EXPRESIÓN ALGEBRAICA
Mucha gente usa recíprocamente expresiones algebraicas y ecuaciones algebraicas, sin saber que estos términos son varios.
Un algebraico es una frase matemática donde un signo igual conecta dos lados de la frase (= -RRB-. Como ejemplo, 3x + 5 = 20 es una ecuación algebraica donde 20 representa el lado derecho (RHS) y también 3x +5 representa el lado izquierdo (LHS) de la fórmula.
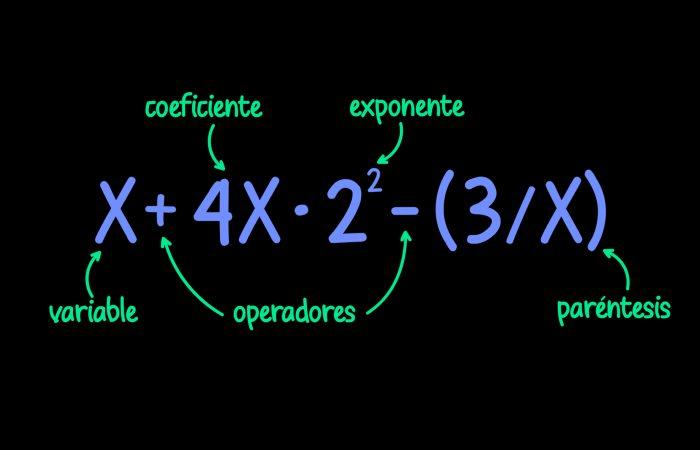
Por el contrario, una expresión algebraica es una expresión matemática donde se incorporan variables y constantes utilizando los símbolos operacionales (+, -, × & ÷). Un símbolo algebraico carece del signo igual (= -RRB-. Por ejemplo, 10x + 63 y también 5x– 3 son instancias de expresiones algebraicas.
Hagamos una evaluación de las terminologías que se utilizan en una expresión algebraica:
- Una variable es una letra cuyo valor desconocemos. Por ejemplo, x es nuestra variable en la expresión: 10x + 63.
- El coeficiente es un valor numérico que se utiliza junto con una variable. Por ejemplo, 10 es la variable en la expresión 10x + 63.
- Un consistente es un término que tiene un valor garantizado. En esta situación, 63 es la constante en una expresión algebraica, 10x + 63.
Hay varios tipos de expresiones algebraicas; sin embargo, el tipo significativo consiste en:
- Expresión algebraica monomial: Este tipo de expresión tiene un solo término, por ejemplo, 2x, 5x 2,3 xy, etc.
- Expresión binomial: Una expresión algebraica que tiene dos términos distintos, por ejemplo, 5y + 8, y +5, 6y3 + 4, etc.
- Expresión polinomial: Ésta es una expresión algebraica con más de un término y con no exponentes de variables. Un ejemplo de una expresión polinomial es músculo abdominal + b c + c a, y así sucesivamente.
Otros tipos de expresiones algebraicas son:
- Expresión numérica: Una expresión matemática incluye tanto números como controladores. No se agrega ninguna variable en una expresión numérica. Ejemplos de expresiones numéricas son; 2 +4, 5-1, 400 +600, etc.
- Expresión variable: Ésta es una expresión que incluye variables junto con números, como 6x + y, 7xy +6, etc.
RESOLVER EXPRESIONES ALGEBRAICAS
La función de resolver una expresión algebraica en una ecuación es descubrir la variable desconocida. Cuando dos expresiones están relacionadas, desarrollan una ecuación y, en consecuencia, resulta menos complicado de abordar para los términos desconocidos.
Para arreglar una fórmula, pero las variables de un lado y las constantes del otro lado. Las variables se pueden separar mediante operaciones aritméticas como mejora, reducción, reproducción, departamento, raíz cuadrada, origen de dados, etc.
Una expresión algebraica siempre es compatible. Esto indica que puede reformular la fórmula intercambiando LHS y RHS.
EJEMPLO 1
Determina el valor de x en la siguiente fórmula
5x + 10 = 50
Solución
- Fórmula proporcionada como 5x + 10 = 50
- Aislar las variables y las constantes;
- Puedes mantener la variable en el LHS así como las constantes en el RHS.
- 5 veces = 50-10
- Resta las constantes;
- 5 veces = 40
- Separa ambos lados por el coeficiente de la variable;
- x = 40/5 = 8
Por esa razón, el valor de x es 8.
EJEMPLO 2
Identifica el valor de y cuando 5y + 45 = 100
Solución
- Separa las variables de las constantes;
- 5 años = 100 -45
- 5 años = 55
- Separa ambos lados por el coeficiente;
- y = 55/5
- y = 11
En álgebra convencional, expresión que especifica una operación a realizar en variables abstractas.
Una expresión que especifica un conjunto de operaciones aritméticas o algebraicas que consta de operadores y operandos y que se puede reducir a un solo resultado numérico cuando se sustituyen los operandos por valores numéricos y se realizan las operaciones especificadas.

