Qué es bisectriz

La bisectriz de ángulo en geometría se refiere a una línea que divide un ángulo en dos ángulos iguales. Antes de hablar de una bisectriz de ángulo, recordemos rápidamente los diferentes tipos de ángulos en matemáticas.

Dependiendo de la inclinación entre los dos brazos, un ángulo puede ser agudo (menos de 90 grados, como un ángulo de 60 grados), obtuso (más de 90 grados) o ángulo recto (exactamente 90 grados).

La construcción de ángulos es una parte importante de la geometría, ya que este conocimiento se extiende también a la construcción de otras figuras geométricas, principalmente los triángulos. Se pueden construir varios ángulos simplemente biseccionando algunos ángulos comunes.

¿QUÉ ES UNA BISECTRIZ DE ÁNGULO?

Una bisectriz de ángulo o la bisectriz de un ángulo es una línea que divide un ángulo en dos partes iguales. Cada ángulo tiene una bisectriz de ángulo. También es la línea de simetría entre los dos brazos de un ángulo, cuya construcción le permite construir ángulos más pequeños.

Supongamos que debe construir un ángulo de 30 °. Esto se puede realizar creando un ángulo de 60 ° y luego bisecándolo. De manera similar, los ángulos de 90 grados, 45 grados, 15 grados y otros se construyen utilizando este concepto.

¿CÓMO CONSTRUIR UNA BISECTRIZ DE ÁNGULO?

Necesitas una regla y una brújula para construir ángulos y sus bisectrices. Dado un ∠PQR conocido o desconocido, los pasos para construir su bisectriz de ángulo son:

Bisectriz

• Paso 1: Coloque el puntero de la brújula en Q y haga un arco que corte los dos brazos del ángulo en dos puntos diferentes.
• Paso 2: Desde el punto donde el primer arco cortó el brazo QP, haga otro arco hacia el interior del ángulo.
• Paso 3: Sin cambiar el radio en la brújula, repita el paso 2 desde el punto donde el primer arco cortó QR.
• Paso 4: Con una regla, dibuje una línea desde Q hasta el punto donde se cruzan los arcos.

La línea que se trazó a través de Q representa la bisectriz del ángulo de ∠PQR.

Nota: Si una bisectriz de ángulo biseca un segmento de línea a 90 °, se conoce como bisectriz perpendicular de esa línea.

LAS BISECTRICES DE ÁNGULO

Para cada ángulo, existe una línea que divide el ángulo en dos partes iguales. Esta línea se conoce como bisectriz de ángulo. En un triángulo, hay tres de esas líneas. Tres bisectrices de un triángulo se encuentran en un punto llamado incentro del triángulo. Hay varias formas de ver por qué esto es así.

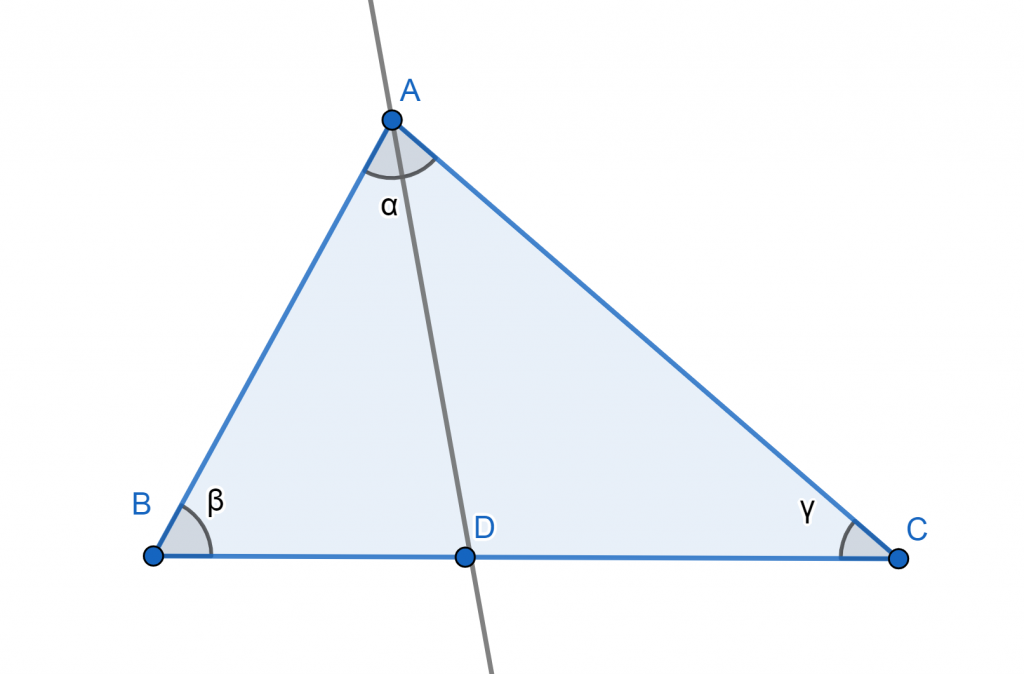
BISECTRICES ANGULARES COMO CEVIANS

Probemos aquí la proporción requerida. Sea AD la bisectriz del ángulo A. El área de un triángulo se puede calcular de muchas maneras. Usaremos dos de ellos para calcular las áreas de los triángulos ABD y ACD. Sea a la mitad del ángulo BAC. Luego:

• Área (ABD) / Área (ACD) = [AB · AD · sen (a) / 2] / [AC · AD · sen (a) / 2] = AB / AC.
• Por otro lado, si AHa es la altitud de A a BC, entonces
• Área (ABD) / Área (ACD) = [AHa · BD / 2] / [AHa · CD / 2] = BD / CD.
• La combinación de los dos da la identidad requerida: AB / AC = BD / CD.

(Se puede encontrar una ilustración dinámica de una prueba diferente en otro lugar. Y hay otra).

VÍA LA TRANSITIVIDAD DE LA IGUALDAD

Se sabe que la bisectriz de un ángulo es el lugar geométrico de los puntos equidistantes de los dos rayos (semilíneas) que forman el ángulo. La existencia del incentro es, entonces, una consecuencia de la propiedad transitoria de la igualdad.

Bisectrices de ángulo como ejes de una línea 2

Si adoptamos la perspectiva de Frank Morley, la transitividad de la igualdad seguirá presente, pero solo implícitamente.

Una bisectriz de ángulo se puede considerar como el lugar geométrico de los centros de los círculos que tocan dos rayos que emanan del mismo punto. En un triángulo, hay tres pares de rayos.

Elige cualquier ángulo y considere su bisectriz. Los círculos que tocan dos lados del ángulo tienen sus centros en la bisectriz. Por el contrario, cualquier punto de la bisectriz sirve como centro de un círculo que toca ambos lados del ángulo.

Considera dos bisectrices de ángulos formados por el par ayb y por el par by c. El círculo con el centro en el punto de intersección de las dos bisectrices toca los tres lados. En particular, toca los lados ayc y, por tanto, tiene su centro en la bisectriz del ángulo formado por estos dos lados.

Bisectrices angulares como altitudes

Las altitudes de un triángulo sirven como bisectrices de ángulo del triángulo órtico asociado. Esta asociación se puede utilizar a la inversa.

Considera ΔABC. A través de cada vértice, dibuje una línea perpendicular a la bisectriz del ángulo correspondiente. Estas tres líneas formarán un triángulo, digamos ΔA’B’C ‘. Tenga en cuenta que, dado que A’B ‘es perpendicular a CLc, ∠BCA’ = ∠ACB ‘. Lo mismo ocurre con los pares de ángulos en los vértices A y B. Llamemos a esto una propiedad del espejo. Como sabemos, el triángulo órtico de ΔA’B’C ‘tiene la propiedad de espejo. Haremos uso de esta observación en breve.

Lo que tenemos que mostrar ahora es que las bisectrices ALa, BLb y CLc pasan por los vértices A ‘, B’ y C ‘, respectivamente.

Supongamos por el contrario, que al menos uno de ellos no pasa por el vértice correspondiente. Entonces, el triángulo órtico de ΔA’B’C ‘no podría coincidir posiblemente con ΔABC.

Pero, asumiendo que son diferentes, en el ΔA’B’C ‘habría dos triángulos inscritos distintos (ABC y el órtico) que poseen la propiedad de espejo. Sin embargo, se puede demostrar que esto es imposible. Solo hay un triángulo con esa propiedad. (Para conocer otras propiedades del triángulo órtico, consulte la discusión sobre el problema de Fagnano).

LA PRUEBA ES BASTANTE SIMPLE

Parece que los ángulos de un triángulo con la propiedad del espejo no son arbitrarios. Cuenta los ángulos en el diagrama. (Dos casos, de triángulos obtusos y de ángulo agudo, deberían considerarse por separado. En el primer caso, en lugar de hablar de triángulos inscritos, deberíamos considerar triángulos con vértices en los lados, o sus extensiones, de un triángulo dado).

Cualquier triángulo con la propiedad de espejo debe tener los mismos ángulos que el triángulo órtico y sus lados paralelos a este último.

Como sugiere el tercer diagrama, esto es claramente imposible para un triángulo diferente al órtico. (Consideraciones similares funcionaron en una de las pruebas del teorema de Morley).

NÚMEROS COMPLEJOS

Como en el estudio de las altitudes, deje que los vértices de un triángulo dado se ubiquen en el círculo unitario. Por conveniencia, consideremos que son cuadrados de números complejos: x12, x22 y x32.

El punto medio del arco x1x2 opuesto al vértice x3 es entonces igual ± x1x2. Y lo mismo ocurre con los puntos medios de los arcos x2x3 y x1x3. Elijamos x1, x2, x3 de manera que todos los signos se consideren «+».