Se conoce cómo regla de tres a aquellas operaciones básicas que funcionan para resolver problemas de proporcionalidad entres tres o más valores. Estos valores que se conocen pero además también existe una incógnita.
La regla de tres es una de las operaciones básicas que todos debemos saber hacer. Es una de las reglas que establece una relación de linealidad entre los valores involucrados para poder obtener luego un valor que es desconocido.
Dicha regla de tres es una fórmula para obtener un cuarto término pero que se determina cuando se ha conocidos los otros tres datos.
LEA TAMBIÉN: LA MATEMÁTICA CLARA GRIMA, ELEGIDA PARA ILUSTRAR LAS CALCULADORAS CASIO
En parte es un tanto molesta, pues se podría pensar que no tiene mucha utilidad. Sin embargo, la regla de tres forma parte de las herramientas básicas y prácticas para la cotidianidad. Pues te funcionará en diferentes ocasiones. Además que es sencillo, funcionará para calcular algo que queremos comprar en el mercado o si se quiere calcular el tiempo para llegar a la estación de bus más próxima.
A continuación te explicaremos cómo son las formulas y métodos para solucionar dichas operaciones y sus diferentes presentaciones.
¿Cómo resolver una regla de tres simple?
Debes saber que existe regla de tres simple, inversa, compuesta y otras. Así que comenzaremos explicamos una simple de manera que puedas tomar el hilo y solucionar las próximas.
Lo primero es saber esta relación entre las variables, donde A es a B lo que C es a x.
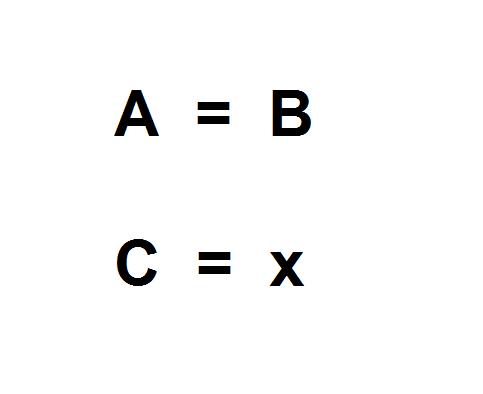
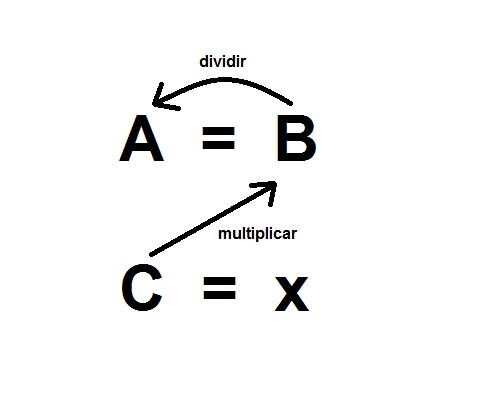
Luego tendrás que despejar la llamada incógnita, es decir, que se debe tratar de buscar el valor de x. Para ello, será necesario tener en cuenta la anterior relación y multiplicar las variables en cruz y dividir por la que queda.
Ahora, tendrás que resolver la siguiente ecuación para resolver la regla de tres que teníamos planteada:
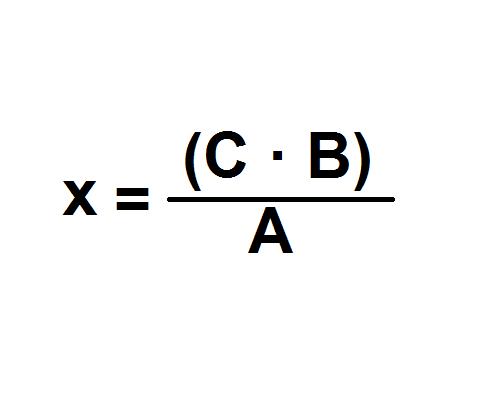
Por ejemplo; si 3 kg de manzanas cuestan 7’55 € ¿cuánto cuestan 4,5 kg?. Entonces lo que se debe hacer es multiplicar los 4’5 kg por 7’55€ y dividirlo después entre los 3 kg, para así saber el valor de x que en este caso corresponde al precio que buscamos.
Realiza las operaciones y el resultado da 11’325€. Como se trata de una moneda, deberemos redondear a dos decimales. Redondea el segundo decimal al alza porque el último decimal es igual o superior a 5, es decir, obtendremos como resultado: 11’33€.
De este modo, tras la solución de la regla se puede decir que 4’5 kg de manzanas tienen un valor total de 11’33€.
Resolviendo una simple directa
En la regla de tres simple directa, en la relación entre los valores, se cumple que:
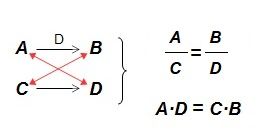
y decimos que A es a B directamente proporcional, como C es a D.
De esta igualdad anterior, se deduce fácilmente que, por ejemplo, si conocemos los valores A, B y C, y queremos calcular D, éste último será:
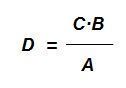
Entonces ponemos de ejemplo que Rosa, debe comprar pintura rosada para darle una mano previa a una habitación que quiere cambiar de color. Si en el bote de pintura se indica que con 1 litro de pintura se pueden pintar 8 m2, ¿cuántos litros necesita teóricamente para pintar las paredes de la habitación si ésta tiene 40 m2 de pared?
Este ejemplo, tiene un punto importante porque la relación de proporcionalidad es directa, ya que cuanto más metros cuadrados de pared se deba pintar más litros de pintura necesitaremos.
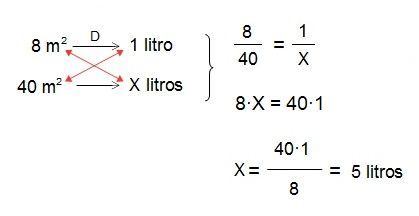
Tras la resolución del problema, decimos entonces que María necesitará, por tanto, 5 litros de pintura.
Regla de tres inversa
Cuando hablamos de la regla de tres simple inversa, decimos que en la relación entre los valores, se cumple que:
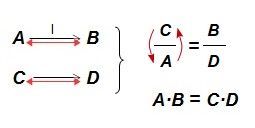
y decimos que A es a B inversamente proporcional, como C es a D. Conocidos los valores A, B y C, el valor D será:
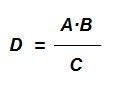
Para la regla de tres inversa tenemos el siguiente ejemplo:
Un grifo con un caudal de salida de agua de 18 litros por minuto tarda 14 horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de 7 litros por minuto?
Decimos entonces que la relación de proporcionalidad es inversa, ya que cuanto más caudal de salida de agua tiene el grifo menos tiempo (en horas) se necesita para llenar el depósito. Por lo tanto decimos a continuación:
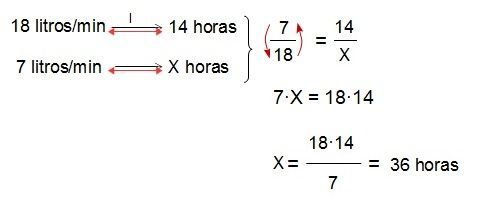
Entonces se deduce tras el resultado, que con un grifo de 7 litros por minuto de caudal (menos caudal) necesitamos 36 horas (más tiempo) para llenar el depósito.
Estas no son las únicas operaciones disponibles, pues algunas veces el problema anunciado puede involucrar más de res cantidades conocidas, además de la desconocida. También hay regla de tres para ello.
Una de las formas rápida de resolver estas situaciones es utilizando una regla de tres compuesta. Esta se compone de varias reglas de tres simples aplicadas sucesivamente.
Como entre las magnitudes se pueden establecer relaciones de proporcionalidad directa o inversa, podemos tener distintos casos.
Cualquier duda extra relacionada con estos casos matemáticos puedes consultar en portales oficiales sobre matemáticas.





